
His math teacher recommended Algebrator, which literally took him through each problem step by step. I feared that he would fall behind in his classes. The \(x\) in the log equation is called the argument and it must be greater than 0, again, to avoid complex numbers.My son was in a major car wreak and was homebound for several months. Also, the base can’t be 1, or the equations wouldn’t be exponential or logarithmic. Note that \(b\) is called the base of the log, and must be greater than 0 (so we don’t have to deal with complex numbers). Remember: A log is in exponent! So when you take the log of something, you are getting back an exponent. The two equations below are two different ways to say the same thing, but the first is an exponential equation, and the second is a logarithmic equation. When doing this, you were adding and subtracting exponents, thus multiplying and dividing large numbers. The numbers on the slide rules had different scales (“logarithmic scales”, meaning that the distance between numbers increase exponentially) and you could simply look up a number, and slide the ruler over to another number to get the number you want. Have you ever heard of a slide rule? (Ask your parents…or grandparents…)Ī slide rule was used (among other things) to multiply and divide large numbers by adding and subtracting their exponents. But logarithms are also used for many other things, including early on to perform computations – before calculators and computers were around. We’ll soon see that Logs can be used to “get the variable in the exponent down” so we can solve for it. I’m not sure exactly why, but you can do so many awesome things with them! I have to admit that logs are one of my favorite topics in math. Introduction to Logarithms (Logs) What is a Log and Why do we Need Them? Inverses of Exponential and Logarithmic Functions (in Inverses Section)īasic Log Properties, including Shortcuts Using Logs (and Exponents) in the Graphing CalculatorĪpplications of Logs, including Half-Life Solving Exponential and Logarithmic Equations using Logs

Applications of Integration: Area and Volume.Exponential and Logarithmic Integration.Riemann Sums and Area by Limit Definition.Differential Equations and Slope Fields.Antiderivatives and Indefinite Integration, including Trig Integration.Derivatives and Integrals of Inverse Trig Functions.Exponential and Logarithmic Differentiation.Differentials, Linear Approximation, and Error Propagation.Curve Sketching, including Rolle’s Theorem and Mean Value Theorem.Implicit Differentiation and Related Rates.Equation of the Tangent Line, Tangent Line Approximation, and Rates of Change.Basic Differentiation Rules: Constant, Power, Product, Quotient, and Trig Rules.Differential Calculus Quick Study Guide.Polar Coordinates, Equations, and Graphs.Law of Sines and Cosines, and Areas of Triangles.Linear and Angular Speeds, Area of Sectors, and Length of Arcs.Conics: Circles, Parabolas, Ellipses, and Hyperbolas.Graphing and Finding Roots of Polynomial Functions.Graphing Rational Functions, including Asymptotes.Rational Functions, Equations and Inequalities.Solving Systems using Reduced Row Echelon Form.The Matrix and Solving Systems with Matrices.Advanced Functions: Compositions, Even and Odd, and Extrema.


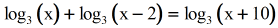
Types of Numbers and Algebraic Properties.Introduction to Statistics and Probability.Powers, Exponents, Radicals (Roots), and Scientific Notation.Multiplying and Dividing, including GCF and LCM.


 0 kommentar(er)
0 kommentar(er)
